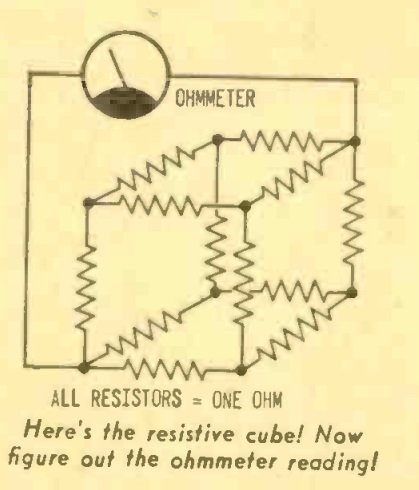
Yesterday, we showed this puzzle from the April-May 1968 issue of Radio TV Experimenter magazine. The question was simple enough–you had to figure out the net resistance between two opposite corners.
Fifty years ago, hobbyists encountering this problem probably started out the way I did, by scribbling the diagram on a piece of paper, trying to flatten it out, and then realizing that the standard equations for series and parallel resistors weren’t really of much help, since they were all hopelessly interlinked.
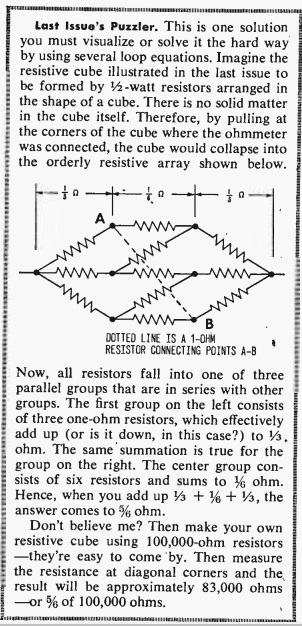
Fifty years ago, the reader had to wait two months for the answer, as shown here in the June-July issue. So I suspect that more than a few got twelve identical resistors, made them into a cube, and then measured.
I didn’t have to do that, because today we have that Google thingie, and I found this solution to the problem, as well as the video shown below, which takes a slightly different approach.
The key to solving this is to notice that the voltage reading at all three of the points marked “A” is the same. And the voltage reading at all three of the points marked “B” is the same. This is because the diagram is symmetrical, and a current flowing from the left to any of the points A is going to pass through an identical resistance. And a current flowing from the right is going to pass through an identical resistor to get to any of the points B.
Since the voltage reading is the same, we can go ahead and make a direct connection between all of the A points, and another direct connection between all of the B points. Since the voltages are the same, no current will flow, and there will be no effect on the circuit.
The effect that it will have, however, is making the problem a lot easier to solve. At this point, we have three resistors on the left, all in parallel. We have six resistors in the middle, all in parallel. And we have three resistors at the right, all in parallel. It’s easy to compute that the equivalent resistances are 1/3, 1/6, and 1/3 ohm. And those values are in series; so we just add them up, and the answer is 5/6 ohms.
This video takes a slightly different approach to arrive at the same answer: