For many years, a standard feature of most radio and electronics magazines was the nomogram (or nomograph).  Before the days of the electronic calculator, it was a convenient way to do calculations of a given formula. The nomogram consisted of three or more scales with the values of a given equation. If you knew two values, you would place a straightedge between them, and the point where the straightedge intersected the third scale, that would be the answer.

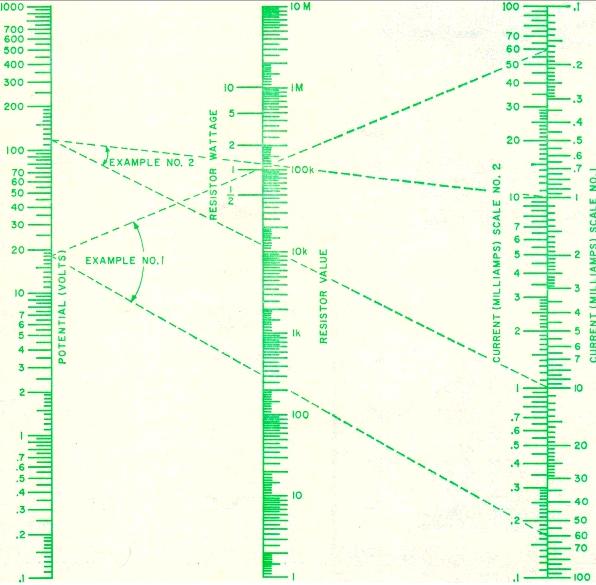
The example at the top of the page is a nomogram of Ohm’s Law, from the April 1967 issue of Electronics World. It shows Ohm’s Law, and it also has superimposed another two scales for calculating the power rating of the resistor. Such graphs were very common. In fact, people cut them out of the magazines for future reference. At one hamfest, I once took home a thick binder labeled “charts and nomos,” in which the previous owner had amassed a large collection of such items.

A nomogram is essentially the same as a slide rule, preset for a particular equation. For recurring problems, even quite complex ones, it was a great time saver.

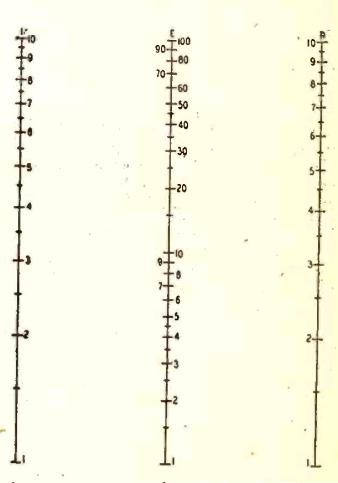
Seventy years ago, Radio Craft Magazine, in its June and July 1946 issues, ran a series on how to make your own nomogram. To illustrate the concept, it started with the simplest possible case, and addition nomograph:

As you can see, this version has three vertical scales, equally spaced. The outer scales have their values placed twice as far apart as the inner scale. To add numbers on the outside scales, you place the straightedge on them, and the point where it intersects the center line is the sum. The concept gets more useful when the linear scales are replaced with logarithmic scales. Now, the nomogram can be used for multiplication, as with a slide rule. The straightedge is placed over the values in the outer scales, and the intersection with the center scale represents the product. Similarly, division can be done by placing the straightedge over one outer scale and the center, and the other scale shows the quotient:

The article showed how to handle exponents by moving the center scale. For example, this graph calculates power from the formula P = I^2 R:

By moving the center scale closer to the current scale, more weight is given to the current. In this case, the current is raised to the power of 2.

The following month’s issue went on to show how to handle more complicated situations, such as reciprocals and square roots. We take for granted these days how easy it is to do calculations with a calculator. But in cases where the same equation had to be repeated over and over, the nomogram represented an easy way to do it with nothing but a straightedge. And making your own nomogram required little more than a few sheets of logarithmic graph paper.

Click Here For Today’s Ripley’s Believe It Or Not Cartoon